
Concept explainers
(a)
The distance moved by the ball
(a)
Answer to Problem 101P
Explanation of Solution
Given: Mass of the ball is
Radius of the ball is
The coefficient of kinetic friction between the ball and the floor is
At the instant the ball touches the floor it is moving horizontally with a speed
Formula used:
Velocity
Equation of kinematics
Where,
Calculation:
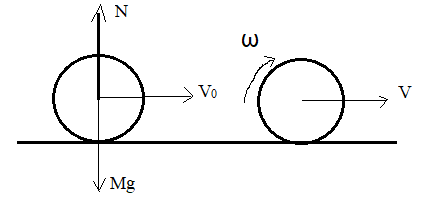
FIGURE:
In the figure
N is the normal reaction force which is acting in the upward direction through the point of contact.
Velocity
In this problem there arise a force of kinetic friction,
This acceleration is in the direction opposite to the direction of motion of the ball and hence equation
The horizontal force
Where,
Thus, the equation
Angular acceleration,
This angular acceleration sets the ball rotating with angular velocity
When the ball starts rolling, the velocity
is satisfied.
Substituting equation
Substituting for
Substituting the expression for
Substituting the value of
The distance moved by the ball
Using the equation
Substituting the expressions for
Conclusion:
The distance moved by the ball before it begin to roll without slipping is
Time taken by the ball to cover the distance
The final speed of the ball is
(b)
The ratio of the final kinetic energy to the initial kinetic energy of the ball.
(b)
Answer to Problem 101P
Explanation of Solution
Given: Mass of the ball is
Radius of the ball is
The coefficient of kinetic friction between the ball and the floor is
At the instant the ball touches the floor it is moving horizontally with a speed
Final velocity of the ball is
Formula used:
The final kinetic energy of the ball is given by,
Where,
Initial kinetic energy of the ball is given by,
Calculation:
Moment of inertia of the ball is given by,
For rotational motion of the ball the velocity,
Substituting for
But,
Therefore final kinetic energy of the ball is,
From equations
Conclusion:
The ratio of the final kinetic energy to the initial kinetic energy of the ball is
(c)
The values of
(c)
Answer to Problem 101P
Explanation of Solution
Given:
Formula used:
Calculation:
Substituting the numerical values in equation
Substituting the numerical values in equation
Substituting the numerical values in equation
Conclusion:
The values of
Want to see more full solutions like this?
Chapter 9 Solutions
Physics for Scientists and Engineers
- A disk 8.00 cm in radius rotates at a constant rate of 1200 rev/min about its central axis. Determine (a) its angular speed in radians per second, (b) the tangential speed at a point 3.00 cm from its center, (c) the radial acceleration of a point on the rim, and (d) the total distance a point on the rim moves in 2.00 s.arrow_forwardA thin rod of length 2.65 m and mass 13.7 kg is rotated at anangular speed of 3.89 rad/s around an axis perpendicular to therod and through its center of mass. Find the magnitude of therods angular momentum.arrow_forwardA solid cylinder of mass 2.0 kg and radius 20 cm is rotating counterclockwise around a vertical axis through its center at 600 rev/min. A second solid cylinder of the same mass and radius is rotating clockwise around the same vertical axis at 900 rev/min. If the cylinders couple so that they rotate about the same vertical axis, what is the angular velocity of the combination?arrow_forward
- Why is the following situation impossible? A space station shaped like a giant wheel has a radius of r = 100 m and a moment of inertia of 5.00 108 kg m2. A crew of 150 people of average mass 65.0 kg is living on the rim, and the stations rotation causes the crew to experience an apparent free-fall acceleration of g (Fig. P10.52). A research technician is assigned to perform an experiment in which a ball is dropped at the rim of the station every 15 minutes and the time interval for the ball to drop a given distance is measured as a test to make sure the apparent value of g is correctly maintained. One evening, 100 average people move to the center of the station for a union meeting. The research technician, who has already been performing his experiment for an hour before the meeting, is disappointed that he cannot attend the meeting, and his mood sours even further by his boring experiment in which every time interval for the dropped ball is identical for the entire evening.arrow_forwardA space station is constructed in the shape of a hollow ring of mass 5.00 104 kg. Members of the crew walk on a deck formed by the inner surface of the outer cylindrical wall of the ring, with radius r = 100 m. At rest when constructed, the ring is set rotating about its axis so that the people inside experience an effective free-fall acceleration equal to g. (See Fig. P10.52.) The rotation is achieved by firing two small rockets attached tangentially to opposite points on the rim of the ring. (a) What angular momentum does the space station acquire? (b) For what time interval must the rockets be fired if each exerts a thrust of 125 N? Figure P10.52 Problems 52 and 54.arrow_forwardDuring a certain time interval, the angular position of a swinging door is described by = 5.00 + 10.0t + 2.00t2, where is in radians and t is in seconds. Determine the angular position, angular speed, and angular acceleration of the door (a) at t = 0 and (b) at t = 3.00 s.arrow_forward
- The propeller of an aircraft accelerates from rest with an angular acceleration = 4t + 6, where is in rad/s2 and t isin seconds. What is the angle in radians through which thepropeller rotates from t = 1.00 s to t = 6.00 s?arrow_forwardThe velocity of a particle of mass m = 2.00 kg is given by v= 5.10 + 2.40 m /s. What is the angular momentumof the particle around the origin when it is located atr= 8.60 3.70 m?arrow_forwardIn testing an automobile tire for proper alignment, a technicianmarks a spot on the tire 0.200 m from the center. He then mountsthe tire in a vertical plane and notes that the radius vector to thespot is at an angle of 35.0 with the horizontal. Starting from rest,the tire is spun rapidly with a constant angular acceleration of 3.00 rad/s2. a. What is the angular speed of the wheel after 4.00 s? b. What is the tangential speed of the spot after 4.00 s? c. What is the magnitude of the total accleration of the spot after 4.00 s?" d. What is the angular position of the spot after 4.00 s?arrow_forward
- A point on a rotating turntable 20.0 cm from the center accelerates from rest to a final speed of 0.700 m/s in 1.75 s. At t = 1.25 s, find the magnitude and direction of (a) the radial acceleration, (b) the tangential acceleration, and (c) the total acceleration of the point.arrow_forwardA turntable (disk) of radius r = 26.0 cm and rotational inertia0.400 kg m2 rotates with an angular speed of 3.00 rad/s arounda frictionless, vertical axle. A wad of clay of mass m =0.250 kg drops onto and sticks to the edge of the turntable.What is the new angular speed of the turntable?arrow_forwardA thin rod of length 2.65 m and mass 13.7 kg is rotated at anangular speed of 3.89 rad/s around an axis perpendicular to therod and through one of its ends. Find the magnitude of the rodsangular momentum.arrow_forward
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning





