
Concept explainers
To find: the extrema’s of given function and sketch it’s graph.
Answer to Problem 1E
The function has no extrema on graph.
Explanation of Solution
Given:
The function is given as:
Step 1:the domain is
Step 2: the x-intercept is
Step 3: The function is neither even nor odd.
Step 4:
Differentiating
Since
Also
Step 5:to find horizontal asymptotes, follow
Thus line
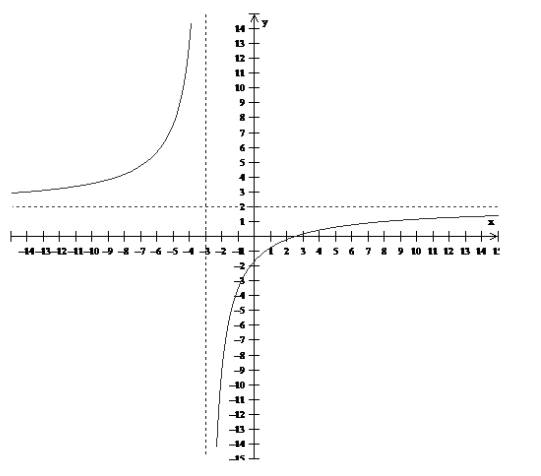
Graph of given function is shown below:
Want to see more full solutions like this?
Chapter 4.5 Solutions
Calculus : The Classic Edition (with Make the Grade and Infotrac)
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
