An Introduction to Thermal Physics
1st Edition
ISBN: 9780201380279
Author: Daniel V. Schroeder
Publisher: Addison Wesley
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 3.4, Problem 34P
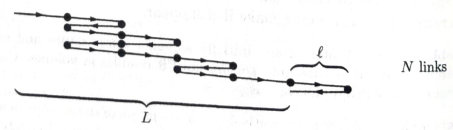
(a) Find an expression for the entropy of this system in term of N and
(b) Write down a formula for L in terms of N and N1,
(c) For a one-dimensional system such as this, the length L is analogous to the volume V of a three-dimensional system. Similarly, the pressure P is replaced by the tension force F. Taking F to be positive when the rubber band is pulling inward, write down and explain the appropriate
(d) Using the thermodynamic Identity, you can flow express the tension force F in terms of a partial derivative of the entropy. From this expression, compute the tension in terms of L, T, N, and
(e) Show that when
(f) Discuss the dependence of the tension force on temperature. If you increase the temperature of a rubber band, does it tend to expand or contract? Does this behavior make sense?
(g) Suppose that you hold a relaxed rubber band in both hands and suddenly stretch it. Would you expect its temperature to increase or decrease? Explain. Test your prediction with a real rubber band (preferably a fairly heavy one with lots of stretch), using your lips or forehead as a thermometer. (Hint: The entropy you computed in part (a) is not the total entropy of the rubber band. There is additional entropy a8sociated with the vibrational energy of the molecules; this entropy depends on U but is approximately independent of L.)
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Problem 1:
This problem concerns a collection of N identical harmonic oscillators (perhaps an
Einstein solid) at temperature T. The allowed energies of each oscillator are 0, hf, 2hf,
and so on.
a) Prove =1+x + x² + x³ + .... Ignore Schroeder's comment about proving
1-x
the formula by long division. Prove it by first multiplying both sides of the
equation by (1 – x), and then thinking about the right-hand side of the resulting
expression.
b) Evaluate the partition function for a single harmonic oscillator. Use the result of
(a) to simplify your answer as much as possible.
c) Use E = -
дz
to find an expression for the average energy of a single oscillator.
z aB
Simplify as much as possible.
d) What is the total energy of the system of N oscillators at temperature T?
1.7 A crystal has a basis of one atom per lattice point and a set of primitive translation
vectors (in A):
c = 1.5(i + j+ k),
a = 3i,
where i, j and k are unit vectors in the x, y and z directions of a Cartesian coordinate
system. What is the Bravais lattice type of this crystal, and what are the Miller indices
of the set of planes most densely populated with atoms? Calculate the volumes of the
primitive unit cell and the conventional unit cell.
b= 3j.
In this and following questions, we develop a model for spontaneous
emission of a photon by a diatomic molecule AB (a model molecule),
which rotates and vibrates. In intermediate calculations, atomic units
(a.u.) will be used: unit of mass = the mass of electron, unit of charge
is the proton charge e, (e is a positive constant so that the charge of
electron is -e). The initial state of the molecule is an excited
rotational (1=1) and excited vibrational state (v=1). We consider a
molecule with the reduced mass µ = 10,000 a.u. (it is similar to the
mass of CO). After emitting a photon, the molecule will go to the 1=0,
v=0 state. The first question is about the model potential of the
molecule. It is represented by a potential of the form:
V(r)
=
C6
p12
C12
p6
"
where r is the distance between A and B in the molecule, C6 and C12
are positive constants (C6 =2 and C₁2-1). This potential has a well
meaning that the molecule is bound. The first thing to do is find
vibrational states of the…
Chapter 3 Solutions
An Introduction to Thermal Physics
Ch. 3.1 - Use Table 3.1 to compute the temperature of solid...Ch. 3.1 - Use the definition of temperature to prove the...Ch. 3.1 - Figure 3.3 shows graphs of entropy vs. energy for...Ch. 3.1 - Can a miserly system, with a concave-up...Ch. 3.1 - Prob. 5PCh. 3.1 - Prob. 6PCh. 3.1 - Prob. 7PCh. 3.2 - Prob. 8PCh. 3.2 - In solid carbon monoxide, each CO molecule has two...Ch. 3.2 - An ice cube (mass 30 g) at 0C is left sitting on...
Ch. 3.2 - In order to take a nice warm bath, you mix 50...Ch. 3.2 - Estimate the change in the entropy of the universe...Ch. 3.2 - When the sun is high in the sky, it delivers...Ch. 3.2 - Experimental measurements of the heat capacity of...Ch. 3.2 - Prob. 15PCh. 3.2 - A bit of computer memory is some physical object...Ch. 3.3 - Prob. 17PCh. 3.3 - Prob. 18PCh. 3.3 - Prob. 19PCh. 3.3 - Prob. 20PCh. 3.3 - Prob. 21PCh. 3.3 - Prob. 22PCh. 3.3 - Prob. 23PCh. 3.3 - Prob. 24PCh. 3.3 - Prob. 25PCh. 3.3 - Prob. 26PCh. 3.4 - What partial-derivative relation can you derive...Ch. 3.4 - A liter of air, initially at room temperature and...Ch. 3.4 - Sketch a qualitatively accurate graph of the...Ch. 3.4 - As shown in Figure 1.14, the heat capacity of...Ch. 3.4 - Experimental measurements of heat capacities are...Ch. 3.4 - A cylinder contains one liter of air at room...Ch. 3.4 - Prob. 33PCh. 3.4 - Polymers, like rubber, are made of very long...Ch. 3.5 - Prob. 35PCh. 3.5 - Prob. 36PCh. 3.5 - Prob. 37PCh. 3.5 - Suppose you have a mixture of gases (such as air,...Ch. 3.6 - Prob. 39P
Additional Science Textbook Solutions
Find more solutions based on key concepts
The independent variable item, constant variable item and dependent variable item from the given figure.
Glencoe Physical Science 2012 Student Edition (Glencoe Science) (McGraw-Hill Education)
Impact Energy. Consider a comet about 2 kilometers across with a mass of 4 × 1012 kg. Assume that it crashes in...
Life in the Universe (4th Edition)
A police officer pulls you over for speeding. He tells you that his radar tracked you moving at a rate of 45mph...
Conceptual Integrated Science
18.(II) (a) Determine the equivalent resistance of the “ladder” of equal 175-? resistors shown in Fig. 19-49. I...
Physics: Principles with Applications
What is the role of “loose” electrons in heat conductors?
Conceptual Physics (12th Edition)
Write each number in scientific notation.
3. 2650
Applied Physics (11th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- The simple mass on a spring is the basis for our description of almost any oscillation. Lets consider the vibrational states of a simple diatomic molecule, say N2. We will model it as two identical masses connected by a spring as shown in the figure at the top right.This is a little different from the cart on a spring since there is no wall -- both of the atoms are moving. But if we only look at oscillations of the molecule where the center of mass is not moving, the atoms are moving equally and oppositely. When one is going left, the other goes an equal amount to the right and vice versa. This is like two carts attached to a wall and oscillating equally and oppositely as shown in the lower picture. The only difference is the way we treat the spring. When each atom moves a distance x, the spring between the atoms actually stretches a distance 2x, so the force on each atom is -2kx. We can therefore model the motion of one of the nitrogen atoms as a single cart on a spring if we…arrow_forwardI'm hoping for a good explanation of how to do this. I'm also wondering why it matters if the configuration is linear or nonlinear? A triatomic molecule can have a linear configuration, as does CO2 (Figure a), or it can be nonlinear, like H2O (Figure b). Suppose the temperature of a gas of triatomic molecules is sufficiently low that vibrational motion is negligible. (a) What is the molar specific heat at constant volume, expressed as a multiple of the universal gas constant (R) if the molecules are linear?Eint/nT = ? (b) What is the molar specific heat at constant volume, expressed as a multiple of the universal gas constant (R) if the molecules are nonlinear?Eint/nT = ? At high temperatures, a triatomic molecule has two modes of vibration, and each contributes 0.5R to the molar specific heat for its kinetic energy and another 0.5R for its potential energy. (c) Identify the high-temperature molar specific heat at constant volume for a triatomic ideal gas of the linear molecules. (Use…arrow_forwardConsider two blocks of copper. Block A contains 800 atoms and initially has a total of 20 quanta of energy. Block B contains 200 atoms and initially has 80 quanta of energy. The two blocks are placed in contact with each other, inside an insulated container (so no thermal energy can be exchanged with the surroundings).After waiting for a long time (for example, an hour), which of the following would you expect to be true? A. The entropy of block A is equal to the entropy of block B. B. Approximately 50 quanta of energy are in block A, and approximately 50 quanta of energy are in block B. C. Approximately 80 quanta of energy are in block A, and approximately 20 quanta of energy are in block B. D. The temperature of block A and the temperature of block B are equal.arrow_forward
- Consider Ω = αU^(αNV) Use the following steps to find T, U(T), and CV 1. Use quantum mechanics and some combinatorics to find an expression for the multiplicity,Ω , in terms of U, V, N, and any other relevant variables. 2. Take the logarithm to find the entropy, S. 3. Differentiate S with respect to U and take the reciprocal to find the temperature, T, as a function of U and other variables. 4. Solve for U as a function of T (and other variables). 5. Differentiate U(T) to obtain a prediction for the heat capacity (with the other variables held fixed).arrow_forwardThree balls (labeled A, B, C) are placed into two different boxes (1 and 2), as in (Figure 1). If all arrangements are equally likely, what is the probability that all three will be in box 1?arrow_forwardWhy is the probability of a system's ground state larger than the probabilities of its excited states for a system in thermal equilibrium with a reservoir? In answering this you may want to consider your calculations in this worksheet. a. Adding energy to the large reservoir increases the total entropy more than adding the same amount of energy to the system. b. Removing all energy from the system increases its entropy the most. c. The probability of the state of the system is maximized when the number of microstates of the system is maximized. d. The probability of the state of the system is maximized when the number of microstates for that state of the system and reservoir is maximized.arrow_forward
- A gas consists of three atoms with access to three different quantum states with the same energy. How many different microstates can be formed from these quantum levels for the case of the Fermi-Dirac gas, where the atoms are differentiated but only one atom is allowed in each state.arrow_forwardThe intensities of spectroscopic transitions between the vibrational states of a molecule are proportional to the square of the integral ∫ψv′xψvdx over all space. Use the relations between Hermite polynomials given in Table 7E.1 to show that the only permitted transitions are those for which v′ = v ± 1 and evaluate the integral in these cases.arrow_forwardShow me the step by step solution. Thank you!arrow_forward
- A system containing a single particle in a rigid container at temperature 100 K has a translational partition function of Ztrans = 1.5 × 1012. (a) If the mass of the particle is doubled, what is the new value for ztrans? Report your answer in scientific notation (in Blackboard, 1.23 x 1045 is written 1.23E45).arrow_forwardConsider N identical harmonic oscillators (as in the Einstein floor). Permissible Energies of each oscillator (E = n h f (n = 0, 1, 2 ...)) 0, hf, 2hf and so on. A) Calculating the selection function of a single harmonic oscillator. What is the division of N oscillators? B) Obtain the average energy of N oscillators at temperature T from the partition function. C) Calculate this capacity and T-> 0 and At T-> infinity limits, what will the heat capacity be? Are these results consistent with the experiment? Why? What is the correct theory about this? D) Find the Helmholtz free energy from this system. E) Derive the expression that gives the entropy of this system for the temperature.arrow_forwardFor an ideal gas of classical non- interacting atoms in thermal equilibrium, the Cartesian component of the velocity are statistically independent. In three dimensions, the probability density distribution of the velocity is: where σ² = kBT m P(Vx, Vy, Vz) = (2nо²)-³/² exp 20² 1. Show that the probability density of the velocity is normalized. 2. Find an expression of the arithmetic average of the speed. 3. Find and expression of the root-mean-square value of the speed. 4. Estimate the standard deviation of the speed.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Modern PhysicsPhysicsISBN:9781111794378Author:Raymond A. Serway, Clement J. Moses, Curt A. MoyerPublisher:Cengage Learning
Modern Physics
Physics
ISBN:9781111794378
Author:Raymond A. Serway, Clement J. Moses, Curt A. Moyer
Publisher:Cengage Learning
The Laws of Thermodynamics, Entropy, and Gibbs Free Energy; Author: Professor Dave Explains;https://www.youtube.com/watch?v=8N1BxHgsoOw;License: Standard YouTube License, CC-BY